Una escala de notas numérica como la que se usa en Chile está definida por estos parámetros:
Estos parámetros determinan los 3 puntos en el siguiente gráfico, que tienen en su eje horizontal \(p\), el puntaje obtenido en la evaluación, y en el vertical \(n\), la nota correspondiente:
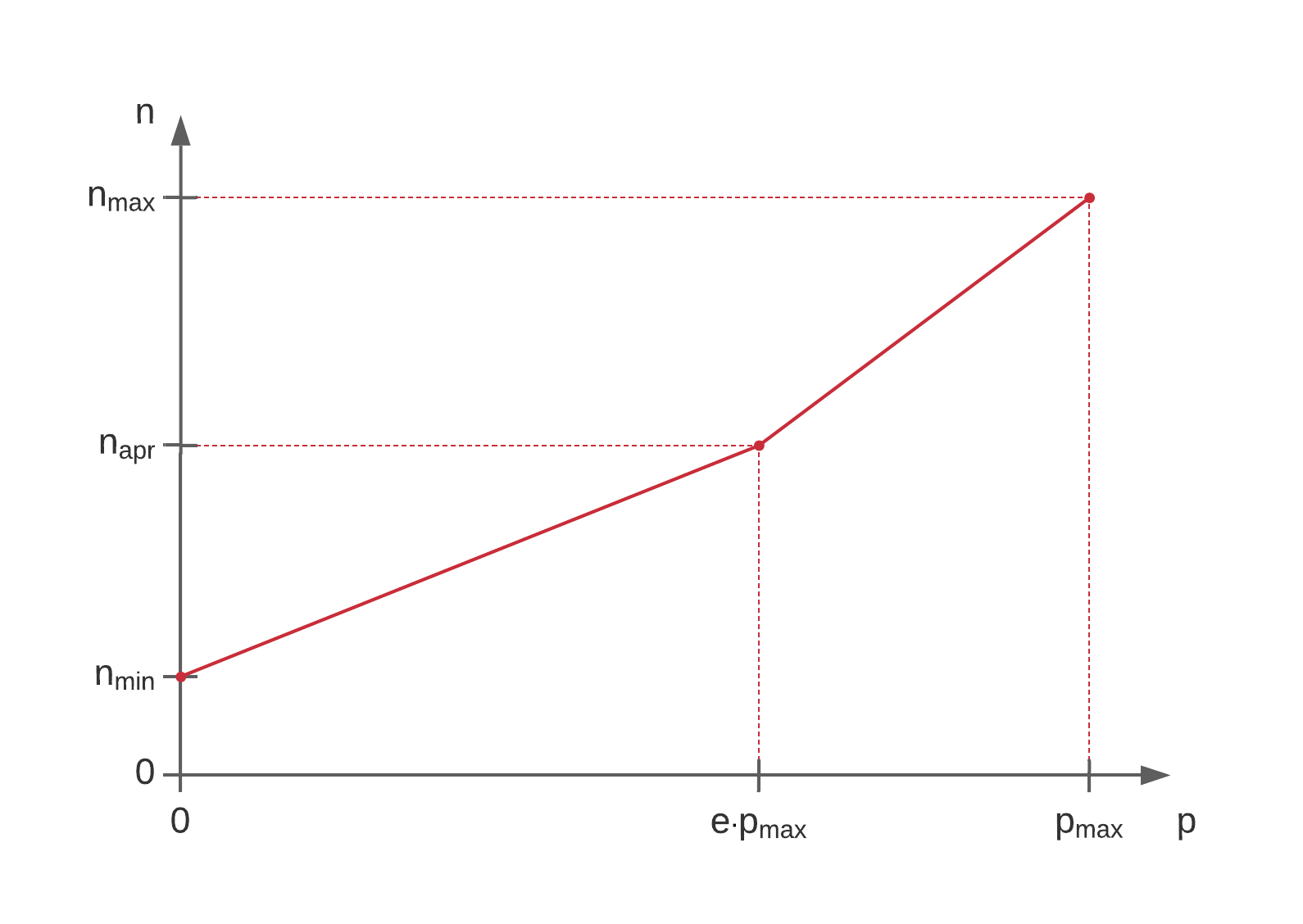
A partir de estos puntos se puede determinar la siguiente fórmula general: \[ n = \begin{cases} (n_{apr}-n_{min}) \cdot \dfrac{p}{e\cdot p_{max}} + n_{min}\text{ si } p<e\cdot p_{max} \\ \\ \\ \\ (n_{max}-n_{apr}) \cdot \dfrac{p-e\cdot p_{max}}{p_{max}\cdot(1-e)} + n_{apr} \text{ si } p \ge e\cdot p_{max} \end{cases} \]
En este caso específico, los parámetros tienen los siguientes valores:
Así, la fórmula específica para esta evaluación queda:
\[ n = \begin{cases} (4.0-1.0) \cdot \dfrac{p}{0.6\cdot 100.0} + 1.0 \text{ si } p<0.6\cdot 100.0 \\ \\ \\ \\ (7.0-4.0) \cdot \dfrac{p-0.6 \cdot 100.0}{100.0\cdot(1-0.6)} + 4.0 \text{ si } p \ge 0.6\cdot 100.0 \end{cases} \]
Reduciendo:
\[ n = \begin{cases} 3.0 \cdot \dfrac{p}{60.0} + 1.0 \text{ si } p<60.0 \\ \\ \\ \\ 3.0 \cdot \dfrac{p-60.0}{40.0} + 4.0\text{ si } p \ge 60.0\end{cases} \]
En este caso particular, \(p=85.0\), que es mayor o igual a 60.0, por lo que corresponde usar la fórmula de abajo:
\[\begin{aligned} n &= 3.0 \cdot \dfrac{p-60.0}{40.0} + 4.0 \\ n &= 3.0 \cdot \dfrac{85.0-60.0}{40.0} + 4.0 \\ n &= 3.0 \cdot \dfrac{25.0}{40.0} + 4.0 \\ n &= 3.0 \cdot 0.625 + 4.0 \\ n &= 1.875 + 4.0 \\ n &= 5.875 \\ \end{aligned} \]
En Chile, corresponde truncar (eliminar los decimales restantes) el resultado a dos decimales (es decir \( n = 5.87\)), y luego aproximar al siguiente decimal si la centésima es mayor o igual a 5. Es decir, finalmente: $$ n = 5.9 $$